KLayout supports a subset of affine transformations with the following contributions:
The execution order is "displacement after rotation, mirroring and scaling". Transformations are used for example to describe the instantiation of a cell. The content of a cell appears in the parent cell after the given transformation has been applied to the content of the cell.
The transformations supported by KLayout cover the transformations employed within GDS2, OASIS and other layout formats. KLayout does not support shearing currently.
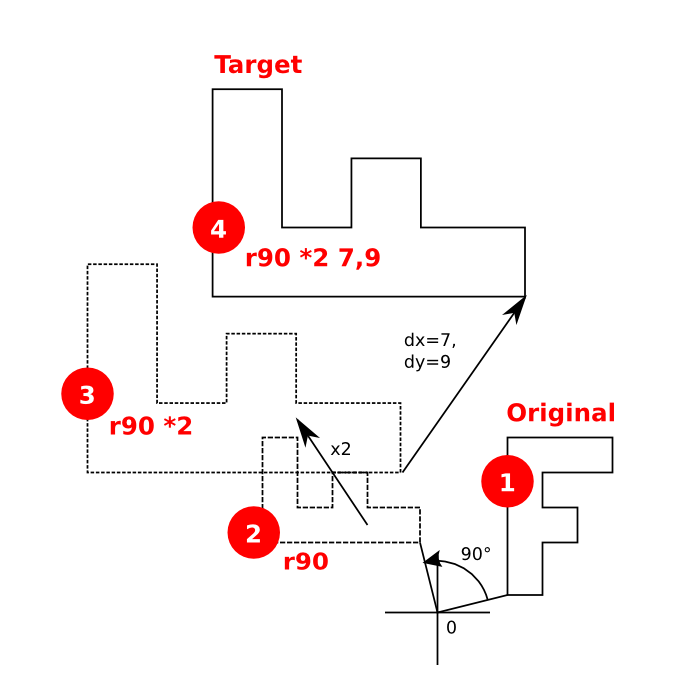
The following figure illustrates the effect of the transformation "r90 *2 7,9". This notation specifies a transformation composed of a rotation by 90 degree, a scaling with factor 2 and a displacement by 7 units in x- and 9 units in y-direction. In that example, the "F" shape is first rotated by 90 degree around the origin. Because the "F" is already displaced from the origin, this will also move the "F" shape. The shape then is scaled. Again it will move because every point of the polygon moves away from the origin. Finally it is displaced by the given displacement vector.

The notation shown here is used in many places within KLayout. It is basically composed of the following parts which are combined putting one or more blanks in between. The order the parts are specified is arbitrary: the displacement is always applied after the rotation.
Here are some examples:
The distance units are usually micron. In some cases (i.e. transformations inside a database), the unit is database units and dx and dy are integer values.
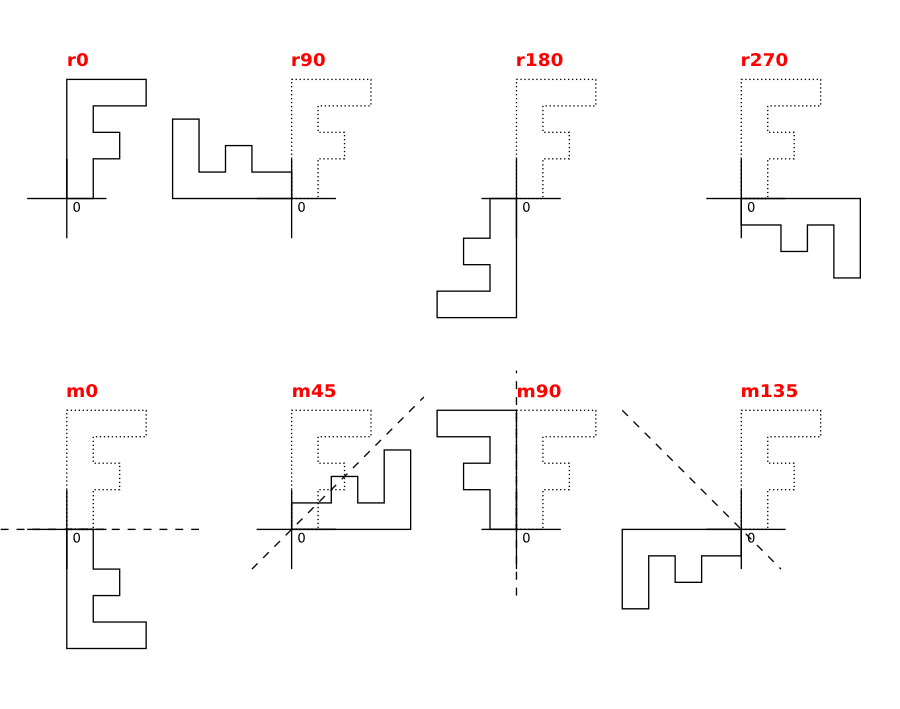
Mirroring and rotation are exclusive and mirroring includes a rotation. In fact, a mirror operation at a certain axis is identical to a mirror operation at the x-axis, followed by a rotation by twice the angle "a". The following figure illustrates rotation and mirroring with the eight basic transformations involving rotations by multiples of 90 degree:
KLayout is not restricted to these basic operations. Arbitrary angles are supported (i.e. "r45" or "m22.5"). Usually however, this implies grid snapping and other issues. This also is true for arbitrary scaling values. KLayout is also more effective when using simple transformations involving only rotations by multiples of 90 degree and do not use scaling.
Note that mirroring at an axis with a given angle "a" is equivalent to mirroring at the x axis followed by a rotation by twice the angle "a". For example:
m45 == m0 followed by r90
When coding transformations, two parameters are used to represent the rotation/mirror part: a rotation angle and a flag indicating mirroring at the x axis. The mirroring is applied before the rotation. In terms of these parameters, the basic transformations are:
| Rotation angle (degree) | Mirror flag = False | Mirror flag = True |
|---|---|---|
| 0 | r0 | m0 |
| 90 | r90 | m45 |
| 180 | r180 | m90 |
| 270 | r270 | m135 |
Transformation objects are convenient objects to operate with. They represent a transformation (technically a matrix) consisting of an angle/mirror and a displacement part. They support some basic operations:
In KLayout there are two two-dimensional coordinate objects: the vector and the point. Basically, the vector is the difference between two points:
v = p2 - p1
Here v is a vector object while p1 and p2 are points.
Regarding transformations, vectors and points behave differently. While for a point, the displacement is applied, it is not for vectors. So
p' = T * p = M * p + d v' = T * v = M * v
Here M is the 2x2 rotation/mirror matrix part of the transformation and d is the displacement vector
The reason why the displacement is not applied to a vector is seen here:
v' = T * v
= T * (p2 - p1)
= T * p2 - T * p1
= (M * p2 + d) - (M * p1 + d)
= M * p2 + d - M * p1 - d
= M * p2 - M * p1
= M * (p2 - p1)where the latter simply is:
v' = M * v
Simple transformations are represented by DTrans or Trans objects. The first operates with floating-point displacements in units of micrometers while the second one with integer displacements in database units. "DTrans" objects act on "D" type floating-point coordinate shapes (e.g. DBox) while "Trans" objects act on the integer coordinate shapes (e.g. Box).
The basic construction parameters of "DTrans" and "Trans" are:
Trans(angle, mirror, displacement) DTrans(angle, mirror, displacement)
"displacement" is a DVector (for DTrans) or a Vector (for Trans).
"angle" is the rotation angle in units of 90 degree and "mirror" is the mirror flag:
| angle | mirror = False | mirror = True |
|---|---|---|
| 0 | r0 | m0 |
| 1 | r90 | m45 |
| 2 | r180 | m90 |
| 3 | r270 | m135 |
Complex transformations in addition to the simple transformations feature scaling (magnification) and arbitrary rotation angles. Other than simple transformations they do not necessarily preserve a grid and rounding is implied. Furthermore they imply a shift is physical scale which renders them difficult to use in physical frameworks (e.g. DRC). Hence their use is discouraged for certain applications.
The basic classes are DCplxTrans for the micrometer-unit (floating-point) version and ICplxTrans for the database-unit (integer) version. The construction parameters are:
ICplxTrans(angle, mirror, magnification, displacement) DCplxTrans(angle, mirror, magnification, displacement)
Here, "angle" is the rotation angle in degree (note the difference to "Trans" and "DTrans" where the rotation angle is in units for 90 degree. "magnification" is a factor (1.0 for "no change in scale").
There are two other variants useful for transforming coordinate systems: CplxTrans takes integer-unit objects and converts them to floating-point unit objects. It can be used to convert from database units to micrometer units when configured with a magnification equal to the database unit value:
T = CplxTrans(magnification: dbu) q = T * p
The other variant is VCplxTrans which converts floating-point unit objects to integer-unit ones. These objects are generated when inverting "CplxTrans" objects.